Big Data in R

Background for the Course

We are going to explore computational principles for understanding data that may be too big to fit in your computers RAM.

The principles extend to data sets that don't fit on a single machine

These slides are available from slides.com here.

The code is available from github here.

Outline for the Course

Processing Data - transform raw data into something we can analyze

Visualizing Data - gain insight with pictorial representations of data

Fitting Data - say statistically rigorous things about data

Which Data?

This course will make use of the Airline OnTime data set.

  - 2009 ASA Stat Computing/Graphics Data Expo

  - All U.S. domestic commercial flights for carriers with

    at least 1% domestic flights for the year.

  - October 1987 - April 2008

  - 29 variables per flight (description for each is here)

  - ~ 12 gigabytes in size (uncompressed)

Is it "Big"?

It is big enough that it's tough to analyze the whole thing on a single laptop.

It is big enough to show how presented tools scale.

It is not so big that we have to wait a long time for processing/visualizing/fitting.

It is publicly available and small enough for you to download.

Setup: Required Packages

install.packages(c("iotools", "rbokeh", 
                   "tidyr", "foreach",
                   "datadr", "trelliscope"))

Put the following in R to install the package we'll need.

Part 1: Processing Data

Setup: Get Airline OnTime

url_prefix="http://stat-computing.org/dataexpo/2009/"

file_nums = as.character(1987:2008)

for (file_num in file_nums) {
  url = paste0(url_prefix, file_num, ".csv.bz2")
  new_file_name = paste0(file_num, ".csv.bz2")
  download.file(url, destfile=new_file_name)
}

Exactly how many flights?

file_names = paste0(1987:2008, ".csv.bz2")

system.time({
  total_lines = 0
  for (file_name in file_names) {
    total_lines = total_lines +
      nrow(read.csv(bzfile(file_name)))
  }
  print(total_lines)})
# [1] 123534969
#     user   system  elapsed 
# 2619.732   49.698 2671.296 

Why is this slow?

1. We are only processing one file at a time.

2. We have to decompress each file.

3. We have to read each file into a data frame.

Process Files in Parallel

library(foreach)
library(doParallel)
cl = makeCluster(4)
registerDoParallel(cl)
system.time({
  total_lines = foreach (file_name=file_names,
                         .combine=`+`) %dopar% {
    nrow(read.csv(bzfile(file_name)))
  }
  print(total_lines)
  stopCluster(cl)
})
# [1] 12​3534969
#   user  system elapsed 

#  0.039   0.107 996.029 ​

Decompress the Files

cl = makeCluster(4)
registerDoParallel(cl)

foreach (file_name=file_names) %dopar% {
  x = read.csv(bzfile(file_name))
  x[,11] = gsub("'", "", x[,11])
  write.csv(x, gsub(".bz2", "", file_name), 
            row.names=FALSE, quote=FALSE)
}
stopCluster(cl)​
file_names = gsub(".bz2", "", file_names)
​

Running time for line count code is now 566.081 seconds.

Use iotools to Read Data

cl = makeCluster(4)
registerDoParallel(cl)
system.time({
  total_lines = foreach(file_name=file_names, 
                        .combine=`+`) %dopar% {

      library(iotools)

      nrow(read.csv.raw(file_name))
    }
stopCluster(cl)​
})

Running time for line count code is now 118.206 seconds.

Can we go any faster?

iotools minimizes overhead from "marshalling"

We can use the save and load functions so that there is no marshalling

We can get the row computation in 63.622 seconds.

It doesn't handle when objects are larger than RAM.

The data representation is specific to R.

Why should we care about counting lines of a file?

Our line counter is scalable

It works on manageable subsets of data

It will run faster as more computing resources available

We can extend it to do more than count lines

Is the average flight delay increasing?

It works on manageable subsets of data

It will run faster as more computing resources available

We can extend it to do more than count lines

What if a file is too big to process?

A quick note on pipes

library(tidyr)

add_one = function(x) x+1
add = function(x, y) x+y 

3 %>% add_one %>% add(10)
# [1] 14

normalize_df = function(x) {
  rownames(x) = NULL
  x$DepTime = sprintf("%04d", x$DepTime)
  x$DepTime = 
    as.numeric(substr(x$DepTime, 1, 2))*60 +
    as.numeric(substr(x$DepTime, 3, 4))
  x
}

file_names = file_names
out_file = file("airline.csv", "wb")
write(paste(col_names, collapse=","), out_file)

for (file_name in file_names) {
  file_name %>% read.csv.raw %>% 
    normalize_df %>% as.output(sep=",") %>% 
    writeBin(out_file)
}
close(out_file)

xs = read.csv("1995.csv", nrows=50, 
              as.is=TRUE)
col_names = names(xs)
col_types = as.vector(sapply(xs, class))

chunk.apply(input="airline.csv",
  FUN=function(chunk) {
    nrow(dstrsplit(chunk, col_types, ","))
  }, CH.MERGE=sum, parallel=6)
​
# [1] 86289324

airline_apply = function(fun, ch_merge=list, 
                         ..., 
                         parallel=6) {
  chunk.apply(input="airline.csv",
​    FUN=function(chunk){
      x = dstrsplit(chunk, col_types, ",")
      names(x) = col_names
      fun(x, ...)
    }, CH.MERGE=ch_merge, 
    parallel=parallel)
}

Let's create some summaries.

Part 2: Visualization

Why do we visualize data?

“There’s nothing better than a picture for making you think of all the questions you forgot to ask” -John Tukey

How do use visualize "big" data

Make the plots interactive.

Make a lot of plots.

An Interactive Visualization Provides

A multi-resolution view of the data

Navigation to the points we are interested in

Extra information for each point

rbokeh

"Bokeh is a visualization library that provides a flexible and powerful declarative framework for creating web-based plots. Bokeh renders plots using HTML canvas and provides many mechanisms for interactivity." -from the rbokeh website

rbokeh

x = read.csv.raw("1995.csv")
x = na.omit(x[x$Month==1 & x$Dest=="JFK",])

figure() %>% 
  ly_hist(ArrDelay, data=x, breaks=40, 
          freq=FALSE) %>%
  ly_density(ArrDelay, data=x)

Arrival vs Departure

figure() %>% 
  ly_points(ArrDelay, DepDelay, data=x, 
            color=UniqueCarrier, 
            hover=list(ArrDelay, DepDelay, 
                       UniqueCarrier, 
                       Origin))

Single Interactive Plot

Doesn't give us all of the information we want.

Each plot gives us ideas for new plots - so let's make a bunch of plots.

How do we get to the plot we want?

“It seems natural to call such computer guided diagnostics cognostics. We must learn to choose them, calculate them, and use them. Else we drown in a sea of many displays” -John Tukey

Trelliscope

"Trelliscope provides a scalable way to break a set of data into pieces, apply a plot method to each piece, and then arrange those plots in a grid and interactively sort, filter, and query panels of the display based on metrics of interest." - Trelliscope project page

library(trelliscope)

x = read.csv.raw("2008.csv")

conn = vdbConn("airline-db", 
               name = "airline-db", 
               autoYes=TRUE)

bdma = divide(x, c("Month", "DayofMonth", 
                   "Dest"))

class(bdma)
# [1] "ddf"      "ddo"      "kvMemory"

length(bdma)
# [1] 103753

bdma[[1]]$key
# [1] "Month= 1|DayofMonth= 1|Dest=ABE"

figure() %>% 
  ly_points(ArrDelay, DepDelay, 
            data=bdma[[1]]$value, 
            color=UniqueCarrier, 
            hover=list(ArrDelay, DepDelay, 
                       UniqueCarrier, 
                       Origin))

Which cognostics should we define?

bdma_cog_fun = function(x) {

  list(num_flights=cog(nrow(x), desc="Flights"),   
       num_airlines=cog(length(unique(x$UniqueCarriers)),
                        desc="Carriers"),
       num_origins=cog(length(unique(x$Origin)), desc="Origins"),
       avg_dist=cog(mean(x$Distance, na.rm=TRUE),
                    desc="Mean Flight Distance"),
       sd_dist=cog(sd(x$Distance, na.rm=TRUE),
                   desc="SD Flight Distance"),
       avg_dep_delay = cog(mean(x$DepDelay, na.rm=TRUE),
                           desc="Mean Dep Delay"),
       avg_arrival_delay = cog(mean(x$ArrDelay, na.rm=TRUE), 
                               desc="Mean Arrival Delay"))
​}

delay_plot = function(x) {
  figure() %>% 
    ly_points(ArrDelay, DepDelay, data=x, 
              color=UniqueCarrier, 
              hover=list(ArrDelay, DepDelay, 
                         UniqueCarrier, Origin))
}

makeDisplay(bdma,
            name="Delays",
            group="DayMonthAirport",
            desc="Delays by Day, Month, and Year",
            panelFn=delay_plot,
            cogFn=bdma_cog_fun)  
view()

Part 3: Fitting (Linear) Models

WHY SHOULD WE CARE ABOUT LINEAR MODELS?

They are old (Gauss 1795, Legendre 1805).

Random Forests (RF) are at least as simple and often do better at prediction.

Deep Learning (DL) dominates vision, speech, voice recognition, etc.

LM generally has lower computational complexity

LM is optimal RF is not

LM can outperform RF for certain learning tasks

RF is more sensitive to correlated noise

LM vs. RF

See most arguments for LM vs RF

We understand characteristics of the space we are in with LM. Not so with DL.

RESULT: We know how things go wrong with LM, not with DL.

LM vs. DL

Figure from Explaining and Harnessing Adversarial Examples by Goodfellow et al.

Breaking DL with Adversarial Noise

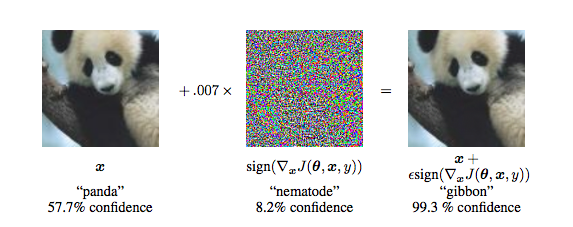
Advantages of (G)LMs

Computationally Efficient

LM is not simply a prediction tool - results are interpretable

Diagnostics for assessing fit and model assumptions

LM is compatible with other models

> train_inds = sample(1:150, 130)
> iris_train = iris[train_inds,]
> iris_test = iris[setdiff(1:150, train_inds),]
> lm_fit = lm(Sepal.Length ~ Sepal.Width+Petal.Length,  
+             data=iris_train)
> sd(predict(lm_fit, iris_test) - iris_test$Sepal.Length)
[1] 0.3879703

> library(randomForest)
> iris_train$residual = lm_fit$residuals
> iris_train$fitted_values = lm_fit$fitted.values
> rf_fit = randomForest(
+   residual ~ Sepal.Width+Petal.Length+fitted_values,  
+   data=iris_train)
> 
> lm_pred = predict(lm_fit, iris_test)
> iris_test$fitted_values = lm_pred
> sd(predict(rf_fit, iris_test)+lm_pred - 
+   iris_test$Sepal.Length)
[1] 0.3458326

> rf_fit2 = randomForest(
+   Sepal.Length ~ Sepal.Width+Petal.Length,
+   data=iris_train)
> sd(predict(rf_fit2, iris_test) - iris_test$Sepal.Length)
[1] 0.40927

THE NOT SO ORDINARY LEAST SQUARES MODEL

Assume

Find

Derivation

What if X isn't full rank?

my_lm = function(X, y) {
  XTy = crossprod(X, y)
  XTX = crossprod(X)
  QR_XTX = qr(XTX)
  keep_vars = QR_XTX$pivot[1:QR_XTX$rank]
  solve(XTX[keep_vars, keep_vars]) %*% 
    XTy[keep_vars]
}

What if X is "almost" not full rank?

my_lm = function(X, y) {
  XTy = crossprod(X, y)
  XTX = crossprod(X)
  QR_XTX = qr(XTX)
  keep_vars = QR_XTX$pivot[1:QR_XTX$rank]
  solve(XTX[keep_vars, keep_vars]) %*% 
    XTy[keep_vars]
}

What is X is "almost" not full rank?

Numerical Stability

x1 = 1:100
x2 = x1 * 1.01 + rnorm(100, 0, sd=7e-6)
X = cbind(x1, x2)
y = x1 + x2 

qr.solve(t(X) %*% X) %*% t(X) %*% y
# Error in qr.solve(t(X) %*% X) : singular matrix 'a' in solve 

beta = qr.solve(t(X) %*% X, tol=0) %*% t(X) %*% y
beta
#         [,1]
# x1 0.9869174
# x2 1.0170043
sd(y - X %*% beta)
# [1] 0.1187066 

sd(lm(y ~ x1 + x2 -1)$residuals)
# [1] 9.546656e-15

Should I include x1 and x2 if they are colinear?

X = matrix(x1, ncol=1) 
beta = solve(t(X) %*% X, tol=0) %*% t(X)%*% y 
beta 
#      [,1] 
# [1,] 2.01 
sd(y - X %*% beta) 
# [1] 6.896263e-06

Implementing OLS with airline_apply