Writing Regression Routines in R

Goals for the talk

 

This talk is is about writing linear regression routines in R and how they fit together

 

I'll cover intuition and implementations

- Ordinary least squares (OLS)

- Ridge Regression

- Generalized Linear Models

- Elastic Net

 

Implementations are meant to be short and readable

 

Anti-Goals 

 

I'm not going to:

- spend a lot of time on statistical properties

- talk about optimality characteristics

- show code that's been optimized for speed

Why should we care about linear models?

 

They are old (Gauss 1795, Legendre 1805).

 

Random Forests (RF) are at least as simple and often do better at prediction.

 

Deep Learning (DL) dominates vision, speech, voice recognition, etc.

LM vs Rf

 

LM generally has lower computational complexity

 

LM is optimal RF is not

 

LM can outperform RF for certain learning tasks

 

RF is more sensitive to correlated noise

LM vs DL

 

See most arguments for LM vs RF

 

 

We understand characteristics of the space we are in with LM. Not so with DL.

RESULT: We know how things go wrong with LM, not with DL.

Breaking DL with Adversarial noise

Figure from Explaining and Harnessing Adversarial Examples by Goodfellow et al.

 

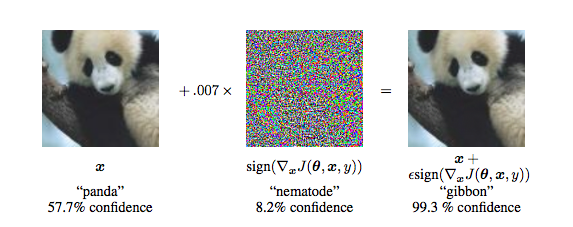
Advantages of LM

Computationally Efficient

 

LM is not simply a prediction tool - results are interpretable

 

Diagnostics for assessing fit and model assumptions

 

LM is compatible with other models

 

> train_inds = sample(1:150, 130)
> iris_train = iris[train_inds,]
> iris_test = iris[setdiff(1:150, train_inds),]
> lm_fit = lm(Sepal.Length ~ Sepal.Width+Petal.Length,  
+             data=iris_train)
> sd(predict(lm_fit, iris_test) - iris_test$Sepal.Length)
[1] 0.3879703
> library(randomForest)
> iris_train$residual = lm_fit$residuals
> iris_train$fitted_values = lm_fit$fitted.values
> rf_fit = randomForest(
+   residual ~ Sepal.Width+Petal.Length+fitted_values,  
+   data=iris_train)
> 
> lm_pred = predict(lm_fit, iris_test)
> iris_test$fitted_values = lm_pred
> sd(predict(rf_fit, iris_test)+lm_pred - 
+   iris_test$Sepal.Length)
[1] 0.3458326
> rf_fit2 = randomForest(
+   Sepal.Length ~ Sepal.Width+Petal.Length,
+   data=iris_train)
> sd(predict(rf_fit2, iris_test) - iris_test$Sepal.Length)
[1] 0.40927

The not so ordinary least squares model

\text{regressor matrix:\ \ } X \in \mathcal{R}^{n \times p}
regressor matrix:  X∈Rn×p\text{regressor matrix:\ \ } X \in \mathcal{R}^{n \times p}
\text{slope coefficients:\ \ } \beta \in \mathcal{R}^p
slope coefficients:  β∈Rp\text{slope coefficients:\ \ } \beta \in \mathcal{R}^p
\text{dependent data:\ \ } y \in \mathcal{R}^n
dependent data:  y∈Rn\text{dependent data:\ \ } y \in \mathcal{R}^n
y = X \beta + \varepsilon
y=Xβ+εy = X \beta + \varepsilon
\min_{\hat{\beta}} ||X \hat \beta - y||^2
minβ^∣∣Xβ^−y∣∣2\min_{\hat{\beta}} ||X \hat \beta - y||^2

Assume

Find

y = X \hat \beta
y=Xβ^y = X \hat \beta
X^T y = X^T X \hat \beta
XTy=XTXβ^X^T y = X^T X \hat \beta
\left(X^T X\right)^{-1} X^T y = \hat \beta
(XTX)−1XTy=β^\left(X^T X\right)^{-1} X^T y = \hat \beta

Derivation

What if X isn't full rank?

my_lm = function(X, y) {
  XTy = crossprod(X, y)
  XTX = crossprod(X)
  QR_XTX = qr(XTX)
  keep_vars = QR_XTX$pivot[1:QR_XTX$rank]
  solve(XTX[keep_vars, keep_vars]) %*% 
    XTy[keep_vars]

}

 

 

What if X is "almost" not full rank?

Numerical Stability

> x1 = 1:100 
> x2 = x1 * 1.01 + rnorm(100, 0, sd=7e-6) 
> X = cbind(x1, x2) 
> y = x1 + x2 
> 
> qr.solve(t(X) %*% X) %*% t(X) %*% y 
Error in qr.solve(t(X) %*% X) : singular matrix 'a' in solve 
> 
> beta = qr.solve(t(X) %*% X, tol=0) %*% t(X) %*% y 
> beta 
        [,1] 
x1 0.9869174 
x2 1.0170043 
> sd(y - X %*% beta) 
[1] 0.1187066 
> 
> sd(lm(y ~ x1 + x2 -1)$residuals) 
[1] 9.546656e-15

Should I include x1 and x2 if they are colinear?

> X = matrix(x1, ncol=1) 
> beta = solve(t(X) %*% X, tol=0) %*% t(X) %*% y 
> beta 
     [,1] 
[1,] 2.01 
> sd(y - X %*% beta) 
[1] 6.896263e-06

Dropping Unbiasedness

We can sometimes get better prediction if we allow some bias (Cramér-Rao bound).

 

Add a parameter α to control bias.

\min_{\hat{\beta}} ||X \hat \beta - y||^2
minβ^∣∣Xβ^−y∣∣2\min_{\hat{\beta}} ||X \hat \beta - y||^2
+ \frac{\lambda}{2}||\hat \beta||^2
+λ2∣∣β^∣∣2+ \frac{\lambda}{2}||\hat \beta||^2

Can be solved with

\hat \beta = \left( X^T X + \frac{\lambda}{2} I \right)^{-1} X^T Y
β^=(XTX+λ2I)−1XTY\hat \beta = \left( X^T X + \frac{\lambda}{2} I \right)^{-1} X^T Y
my_ridge = function(X, y, lambda) {
  XTy = crossprod(X, y)
  XTX = crossprod(X)
  QR_XTX = qr(XTX)
  keep_vars = QR_XTX$pivot[1:QR_XTX$rank]
  solve(XTX[keep_vars, keep_vars] + 
    lambda*diag(length(keep_vars)) %*% 
    XTy[keep_vars]
}

Adding model selection

We can select which regressors do a good job predicting the dependent variable by adding another constraint

\min_{\hat{\beta}} ||X \hat \beta - y||^2 + (1-\alpha) \frac{\lambda}{2} ||\hat \beta||^2 + \alpha \lambda ||\hat \beta||_1
minβ^∣∣Xβ^−y∣∣2+(1−α)λ2∣∣β^∣∣2+αλ∣∣β^∣∣1\min_{\hat{\beta}} ||X \hat \beta - y||^2 + (1-\alpha) \frac{\lambda}{2} ||\hat \beta||^2 + \alpha \lambda ||\hat \beta||_1

The Ridge Part

The Least Absolute Shrinkage and Selection Operator (LASSO) Part

my_lmnet = function(X, y, lambda, alpha, maxit=10000, tol=1e-7) {
  beta = beta_old = rep(0, ncol(X))
  quad_loss = Inf
  for(j in 1:maxit) {
    quad_loss_old = quad_loss
    beta = coordinate_descent(X, y, lambda, alpha, beta_old)
    quad_loss = quadratic_loss(X, y, lambda, alpha, beta)
    if(quad_loss > quad_loss_old) break

    beta = beta_old
  }
  list(beta=beta_old, iterations=j)
}

coordinate_descent = function(X, y, lambda, alpha, beta_old, 
                              W=rep(1,nrow(X)) {
  beta = beta_old
  for (l in 1:length(beta)) {
    beta[l] = soft_thresh(sum(W*X[,l]*(y - X[,-l] %*% beta_old[-l])),
                          sum(W)*lambda*alpha)
  }
  beta / (colSums(W*X^2) + lambda*(1-alpha))
}

soft_thresh = function(x, g) {
  x = as.vector(x)
  x[abs(x) < g] = 0
  x[x > 0] = x[x > 0] - g
  x[x < 0] = x[x < 0] + g
  x
}

quadratic_loss = function(X, y, lambda, alpha, beta, W=1) {
  -1/2/nrow(X) * sum(W*(z - X %*% beta)^2) + 
    lambda * (1-alpha) * sum(beta^2)/2 + alpha * sum(abs(beta))
}
 ​

how do we get from lmnet to glmnet?

A little bit about the glm

\min_{\hat \beta} ||W^{1/2} (y - g(X\hat\beta))||^2
minβ^∣∣W1/2(y−g(Xβ^))∣∣2\min_{\hat \beta} ||W^{1/2} (y - g(X\hat\beta))||^2

- g is the link function

- Element of W are inversly proportional to variance of response which depend on slope coefficients

- See Bryan's notes for more explanation

my_glm = function(X, y, family=binomial, maxit=25, tol=1e-08) {
  beta = rep(0,ncol(A))
  for(j in 1:maxit) {
    eta      = X %*% beta
    g        = family()$linkinv(eta)
    gprime   = family()$mu.eta(eta)
    z        = eta + (y - g) / gprime
    W        = as.vector(gprime^2 / family()$variance(g))
    beta_old = beta
    beta     = solve(crossprod(X,W*X), crossprod(X,W*z), 
                     tol=2*.Machine$double.eps)
    if(sqrt(crossprod(beta-beta_old)) < tol) break
  }
  list(beta=beta, iterations=j)
}

IRLS

Now back to glmnet

my_glmnet = function(X, y, family=binomial, maxit=25, tol=1e-08) {
  beta = rep(0,ncol(X))
  for(j in 1:maxit) {
    eta      = X %*% beta
    g        = family()$linkinv(eta)
    gprime   = family()$mu.eta(eta)
    z        = eta + (y - g) / gprime
    W        = as.vector(gprime^2 / family()$variance(g))
    beta_outer_old = beta
    quad_loss = Inf
    for(k in 1:maxit) {
      beta_inner_old = beta
      quad_loss_old = quad_loss
      beta = coordinate_descent(X, z, lambda, alpha, beta_old, W)
      quad_loss = quadratic_loss(X, z, lambda, alpha, beta, W)
      if(quad_loss > quad_loss_old) break
      beta = beta_inner_old
    }
    if(sqrt(crossprod(beta_inner_old-beta_outer_old)) < tol) break
  }
  list(beta=beta_inner_old)
}

Wrapping up

Currently working on an out-of-core version ioregression.

 

I'll talk about making this fast at RFinance.

 

Thanks to Bryan Lewis for the GLM notes.

 

Thanks to AT&T Labs Research (Taylor Arnold and Simon Urbanek) for helping to make this happen.

 

THanks

Boston R User Group 4/20/2016

By Michael Kane

Boston R User Group 4/20/2016

  • 3,479

More from Michael Kane