Scalable, Exact Approaches to Fitting Linear Models when n >> p

Michael Kane, Taylor Arnold, and Simon Urbanek

iotools provides

  • A framework for computing on streamed chunks of data 

  • Optimized routines for moving data from disk to processor

Let's build a regression library on top of it!

The design of ioregression

  • Build regression preprocessors, kernels, and combiners for different types of linear regressions.

  • Use iotools to stream data to the kernels and aggregate the results to get regression coefficients and diagnostics.

Why not just use foreach?

ioregression is foreach compatible

foreach doesn't give you

  • optimized io routines

  • Doesn't currently handle Hadoop's data locality

Goal is to provide numerical operations required for chunk-wise regressions.

Why linear regressions?

Linear Regressions are Simple

  • Assumptions are known

  • Diagnostics for assessing fit and assumptions

  • Results are interpretable

Linear Regressions are Computationally Efficient

  • Complexity is O(np^2)

  • Model fitting can be parallelized

Linear Regressions are Compatible with Other Analyses

> train_inds = sample(1:150, 130)
> iris_train = iris[train_inds,]
> iris_test = iris[setdiff(1:150, train_inds),]
> lm_fit = lm(Sepal.Length ~ Sepal.Width+Petal.Length,  
+             data=iris_train)
> sd(predict(lm_fit, iris_test) - iris_test$Sepal.Length)
[1] 0.3879703


> library(randomForest)
> iris_train$residual = lm_fit$residuals
> iris_train$fitted_values = lm_fit$fitted.values
> rf_fit = randomForest(
+   residual ~ Sepal.Width+Petal.Length+fitted_values,  
+   data=iris_train)
> 
> lm_pred = predict(lm_fit, iris_test)
> iris_test$fitted_values = lm_pred
> sd(predict(rf_fit, iris_test)+lm_pred - iris_test$Sepal.Length)
[1] 0.3458326
> rf_fit2 = randomForest(
+   Sepal.Length ~ Sepal.Width+Petal.Length,
+   data=iris_train)
> sd(predict(rf_fit2, iris_test) - iris_test$Sepal.Length)
[1] 0.40927

Calculating the OLS slope coefficients

> x1 = 1:100
> x2 = x1 * 1.01 + rnorm(100, 0, sd=7e-6)
> X = cbind(x1, x2)
> y = x1 + x2
> 
> qr.solve(t(X) %*% X) %*% t(X) %*% y
Error in qr.solve(t(X) %*% X) : singular matrix 'a' in solve
> 
> beta = qr.solve(t(X) %*% X, tol=0) %*% t(X) %*% y
> beta
        [,1]
x1 0.9869174
x2 1.0170043
> sd(y - X %*% beta)
[1] 0.1187066
> 
> sd(lm(y ~ x1 + x2 -1)$residuals)
[1] 9.546656e-15

What if we think of x1 and x2 as being highly correlated instead?

> X = matrix(x1, ncol=1)
> beta = qr.solve(t(X) %*% X, tol=0) %*% t(X) %*% y
> beta
     [,1]
[1,] 2.01
> sd(y - X %*% beta)
[1] 6.896263e-06

What does this buy us?

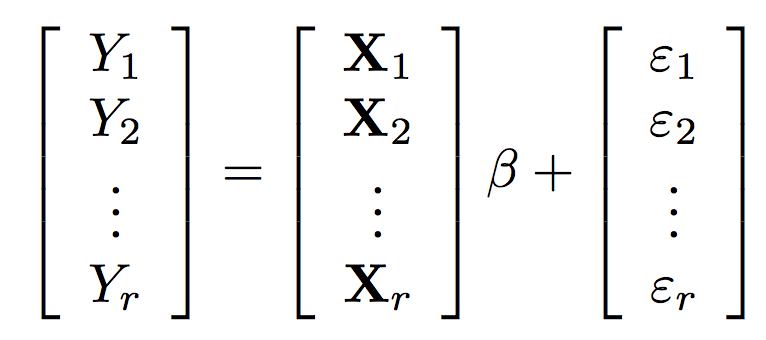
The regression calculation becomes

\hat{\beta} = \left(\sum_{i=1}^r X_i^T X_i \right)^{-1} \left(\sum_{i=1}^r X_i^T Y_i\right)
​β​^​​=(∑​i=1​r​​X​i​T​​X​i​​)​−1​​(∑​i=1​r​​X​i​T​​Y​i​​)

It is easy to implement OLS (and other regressions) in an embarrassingly parallel way.

How do I use it?

library(ioregression)
file_name = "2008.csv"
data = adf(file_name, sep=",", header=TRUE)
system.time({iofit = iolm(DepDelay ~ Distance, data=data)})
##    user  system elapsed 
## 124.884   2.810 127.802

How fast is lm?

system.time({
df = read.table(file_name, header=TRUE, sep=",")
lmfit = lm(DepDelay ~ Distance, data=df)
})
##    user  system elapsed 
## 134.436   3.577 138.258

Status

Under development

  • Routines:
    • OLS 
    • Ridge
    • LARS
    • GLM
    • glmnet (coming)
  • Platforms
    • iotools (done)
    • others?

github.com/kaneplusplus/ioregression

Scalable, Exact Approaches to Fitting Linear Models when n >> p

By Michael Kane

Scalable, Exact Approaches to Fitting Linear Models when n >> p

  • 2,100

More from Michael Kane