Latent Space Approaches to Subtyping in Oncology Trials

Michael Kane and Brian Hobbs

Outline

Motivation: the "new" way clinical oncology trials are being conducted

 

The patient heterogeneity problem

 

Automated subtyping using latent space methods

 

Case study: predicting patient response by subtype

 

Case study: diagnosing mis-dosing based on adverse events

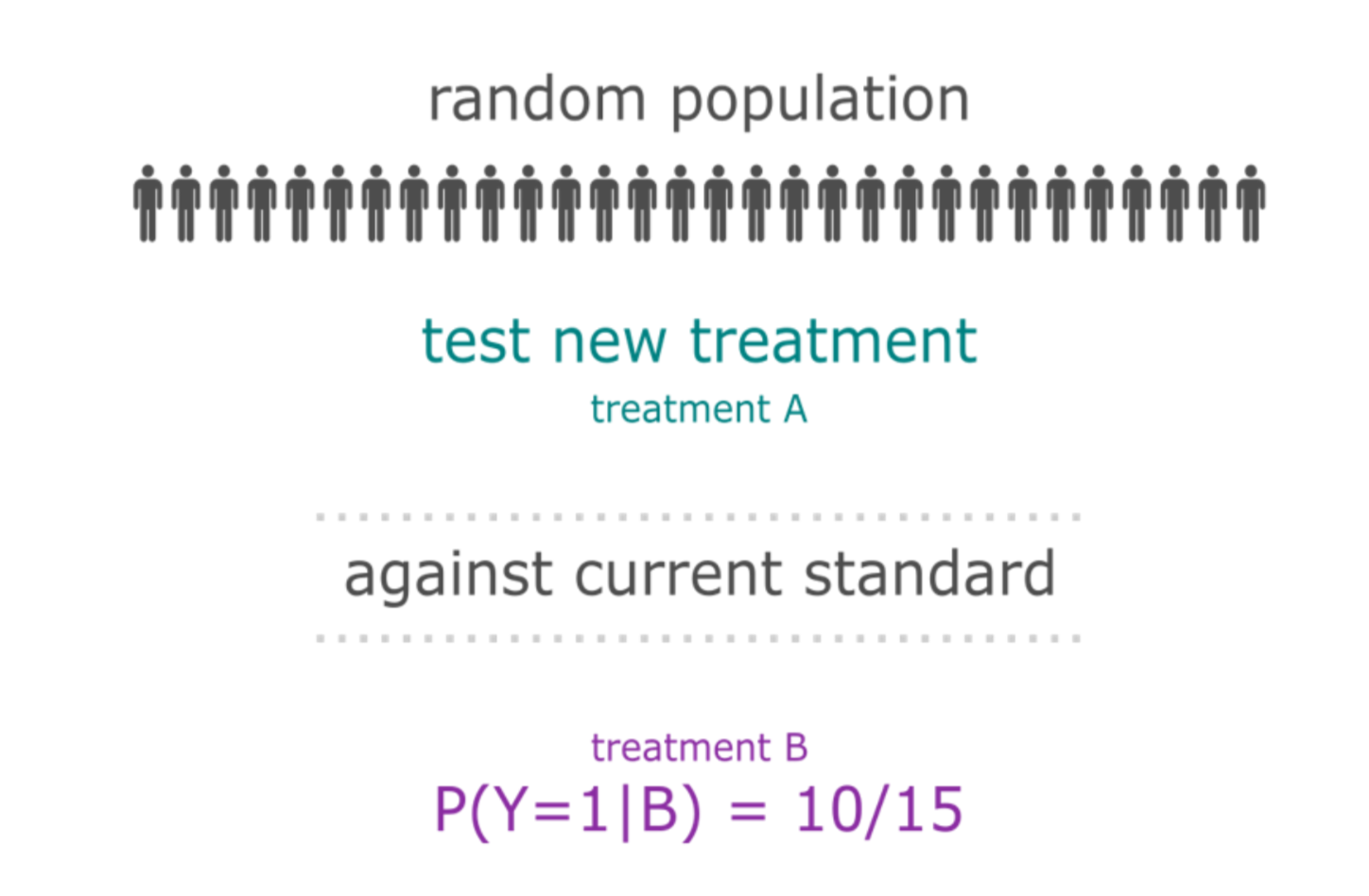
The "old" way of conducting clinical trials

New compound is developed and is thought to deliver a (small) benefit over current therapies for a specific histology

 

A large number of patients are enrolled (at least hundreds)

 

The response rate of the treatment population is tested against a control group

Entrectinib: Patient X Before

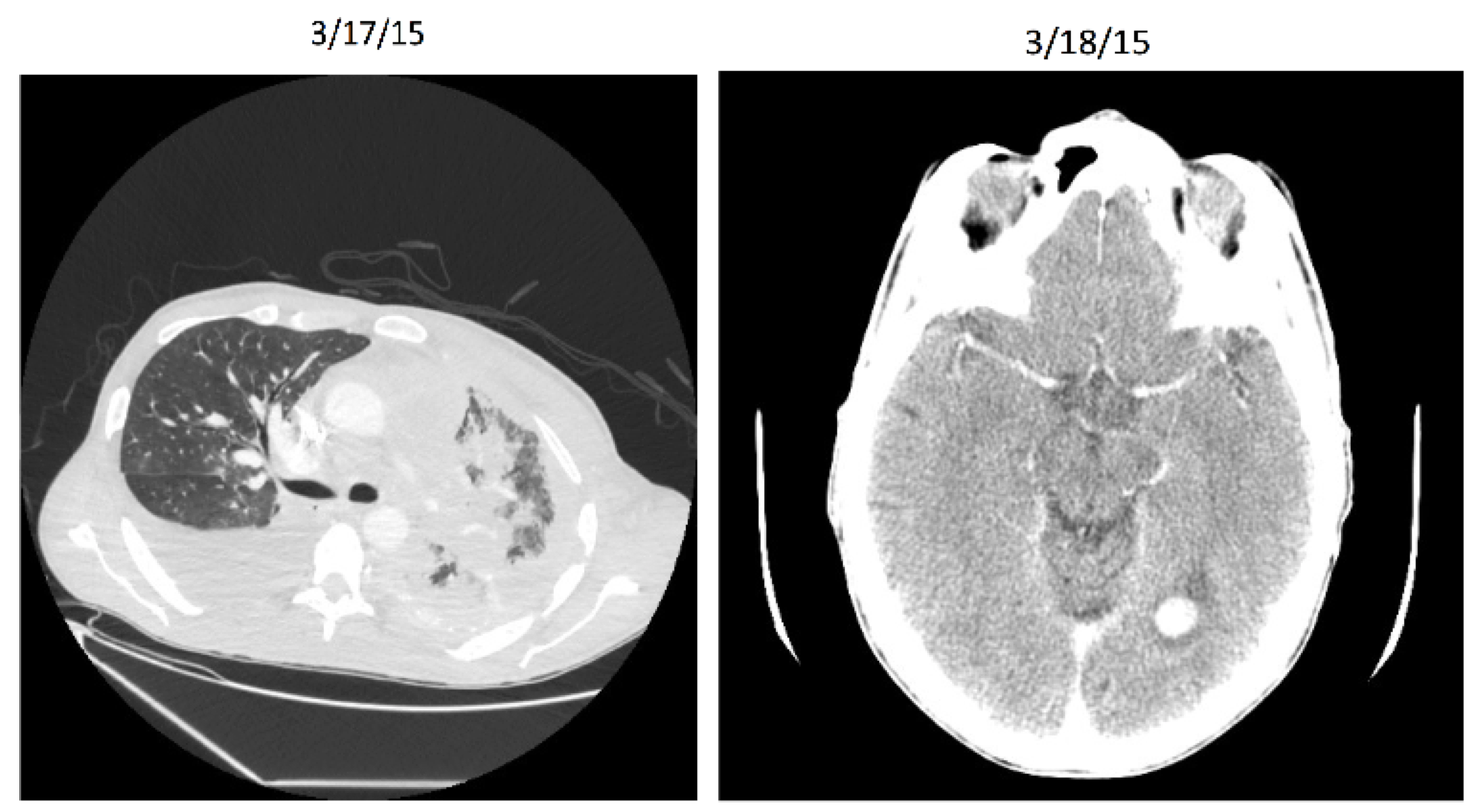
Entrectinib: Patient X After

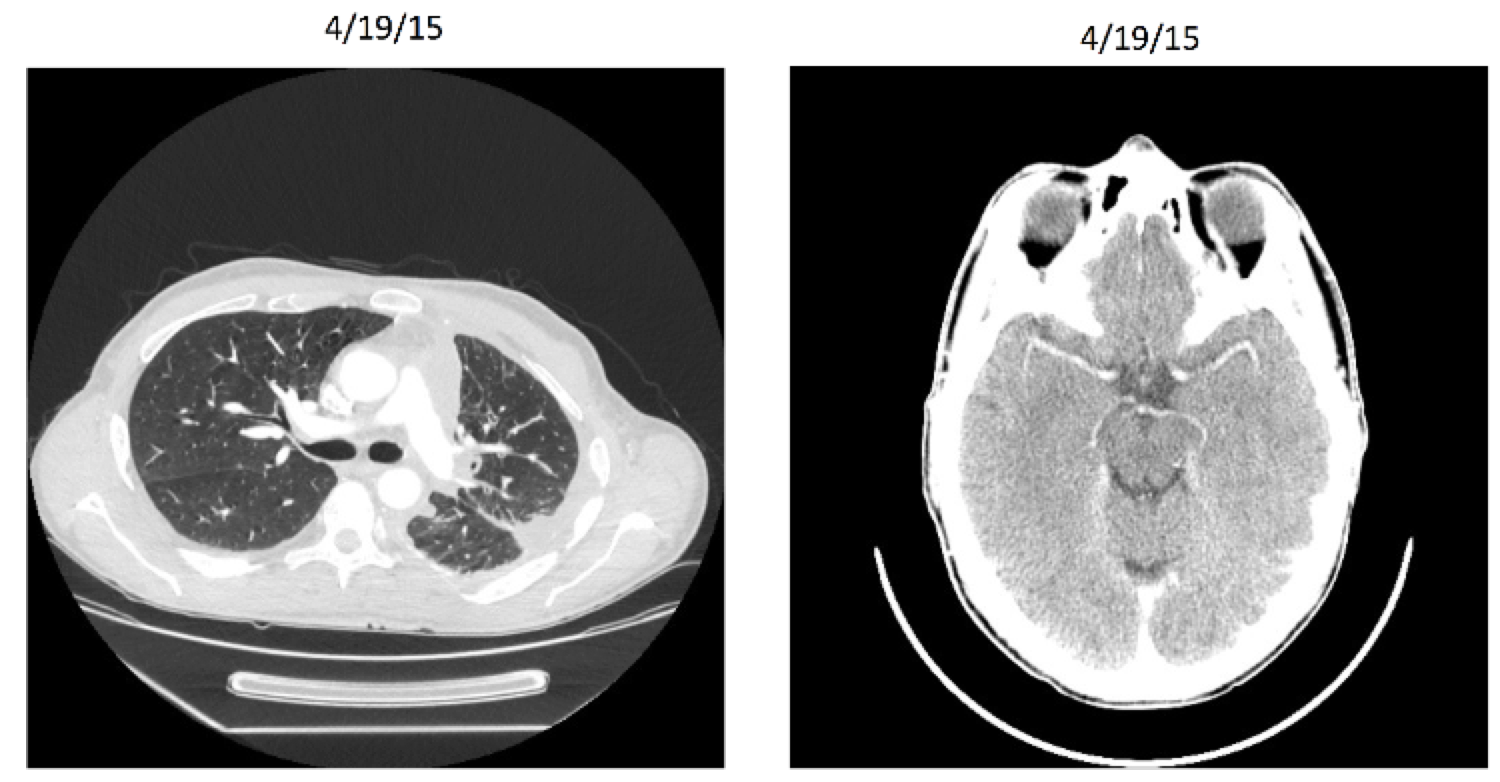
Entrectinib

Targeted therapy (NTRK gene rearrangement)

 

Very stringent inclusion/exclusion criteria

 

Effective for other histologies (including breast, colorectal, and neuroblastoma)

 

8/11 responders for lung cancer in initial study

Breakthrough Trials

"A drug that is intended to treat a serious condition AND preliminary clinical evidence indicates that the drug may demonstrate substantial improvement on a clinically significant endpoint(s) over available therapies"

 

Benefits:

  • Priority review: expedited approval process
  • Rolling reviews, smaller clinical trials, and alternative trial designs

Alternative Designs

Often means single arm

 

Smaller populations

 

May include multiple histologies

 

Still work within FDA regulation, often including "all-comers"

Biomarker Tumor Type Drug N ORR (%) PFS (months)
BRAF V600 NSCLC (>1 line) Dabrafenib + Trametinib 57 63 9.7
ALK fusions NSCLC (prior criz) Brigatinib 110 54 11.1
ALK fusions NSCLC (prior criz Alectinib 225 46-48 8.1-8.9
EGFR T790M NSLCLC (prior TKI) Osimertinib 127 61 9.6
BRCA 1/2 Ovarian (>2 prior) Rucaparib 106 54 12.8
MSI-H/MMR-D Solid Tumor Pembroliumab 149 40 Not reached
BRAF V600 Erdheim Chester Vemurafinib 22 63 Not reached

Breakthrough Therapies

The patient heterogeneity problem

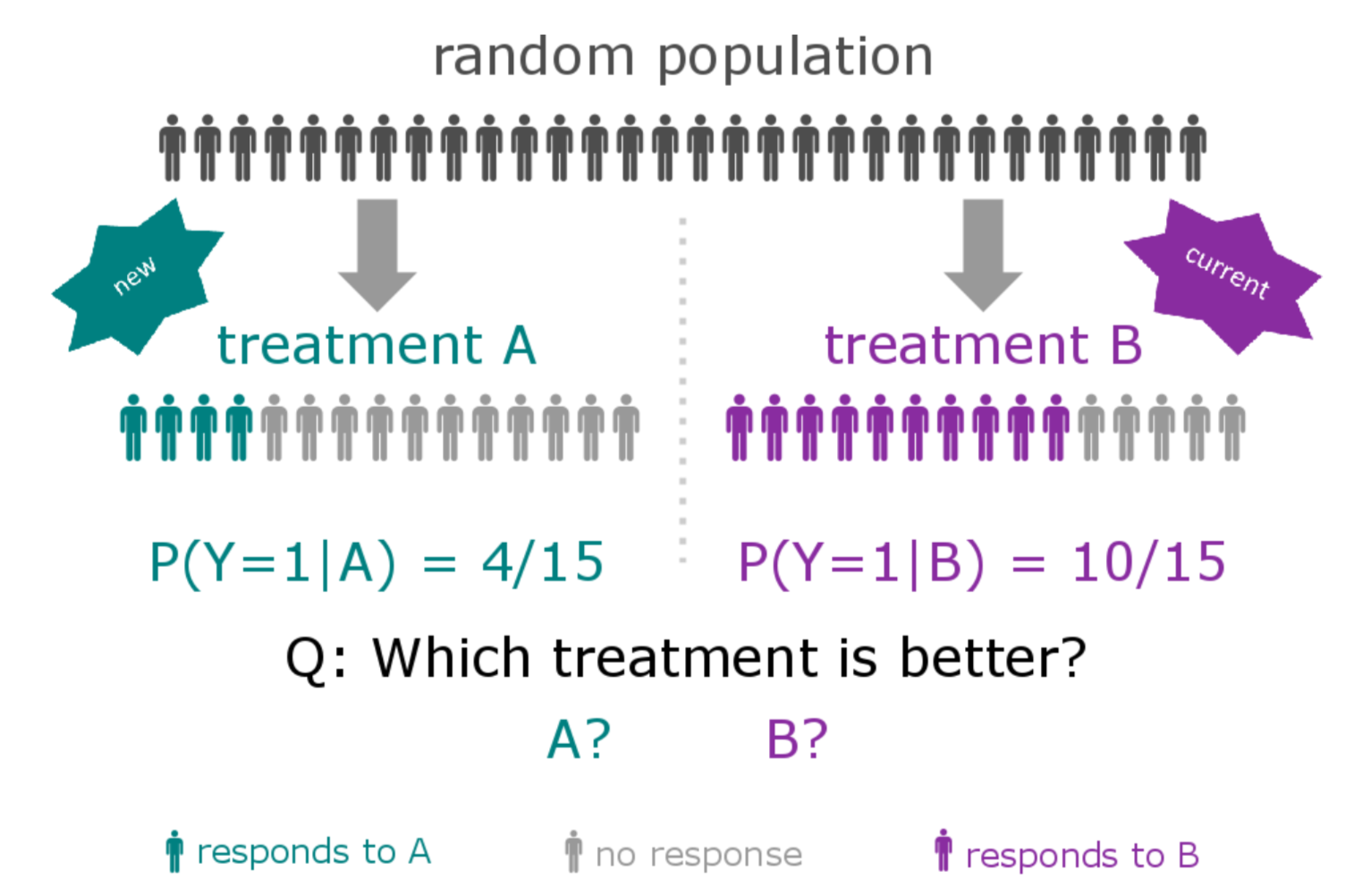
The patient heterogeneity problem

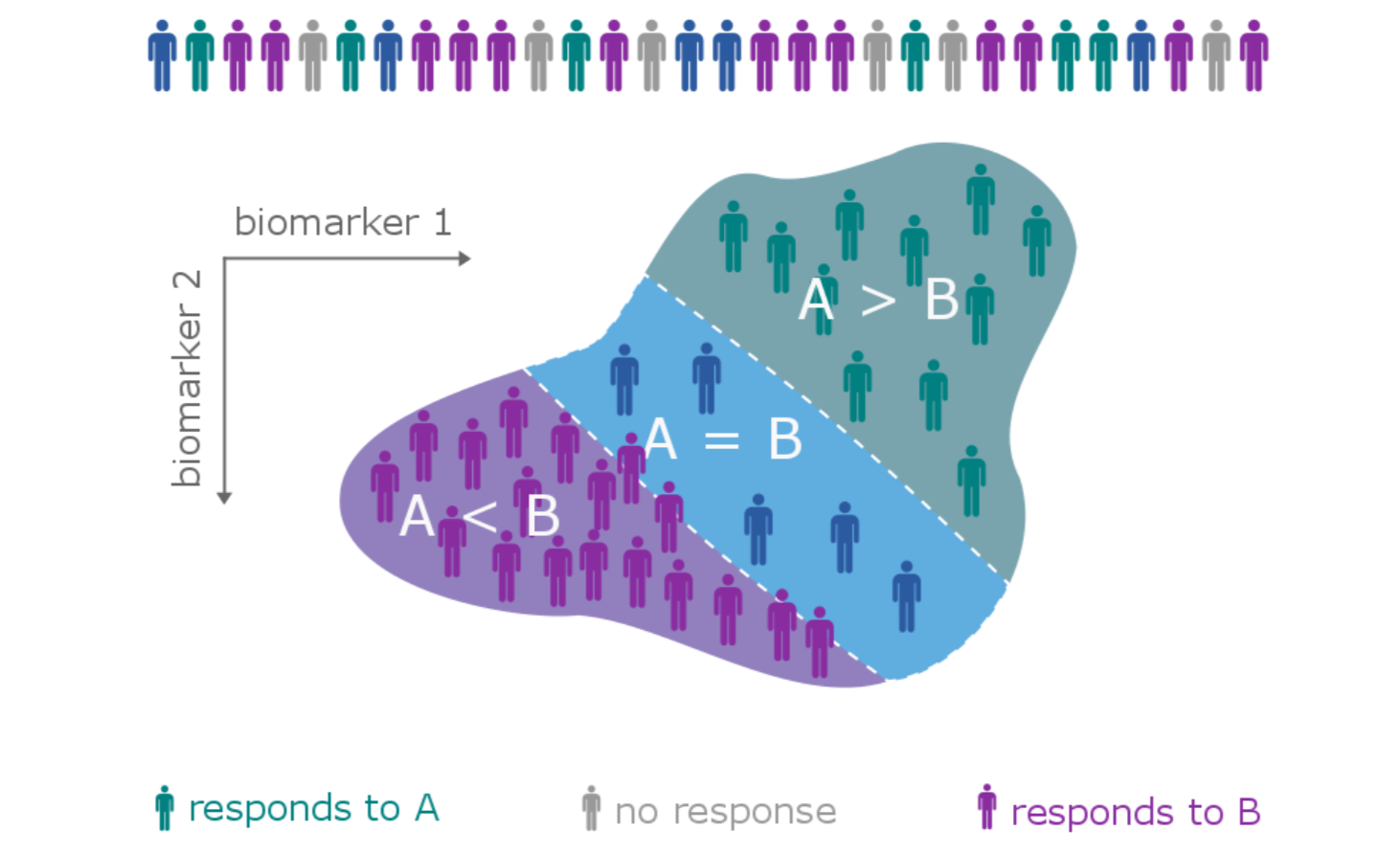
The patient heterogeneity problem

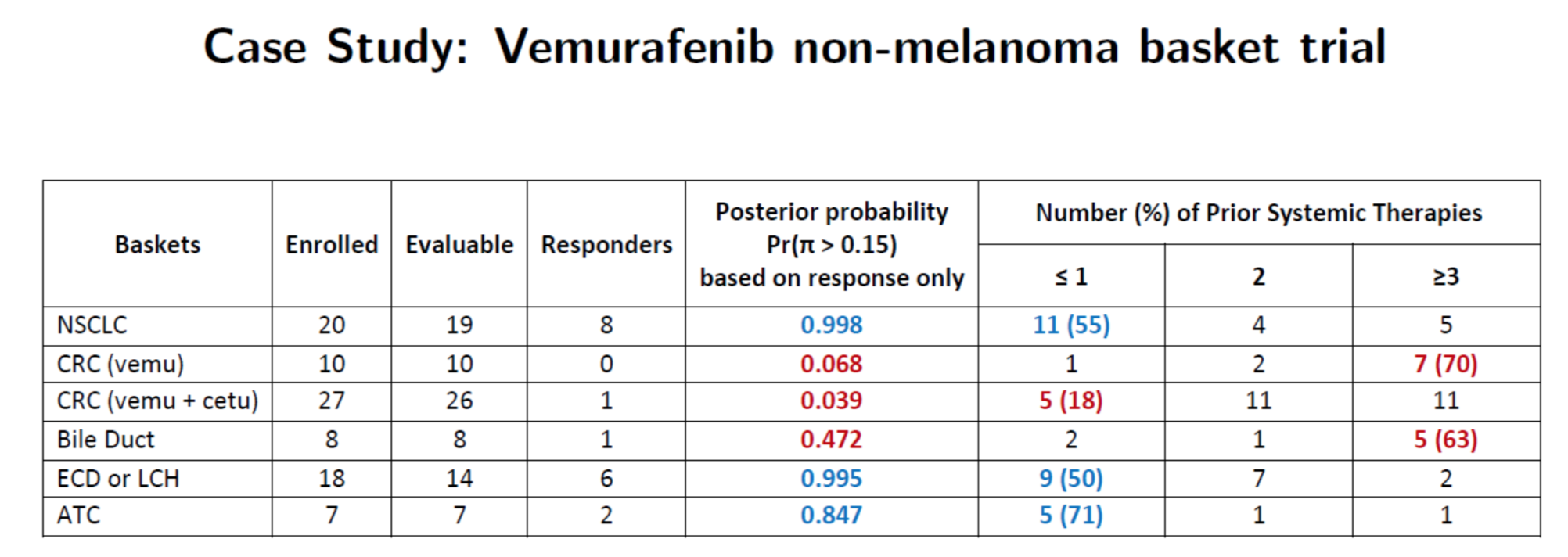
Hobbs, Kane, Hong, and Landin. Statistical challenges posed by basket trials: sensitivity analysis of the Vemurafinib study. Accepted to the Annals of Oncology.

A subtype is a group of patients with similar, measurable characteristics who respond similarly to a therapy.

Why isn't supervised learning enough?

> summary(lm(y ~ x1n + x2n - 1, ts1))

Call:
lm(formula = y ~ x1n + x2n - 1, data = ts1)

Residuals:
   Min     1Q Median     3Q    Max
-7.276 -2.695  0.260  2.341  7.358

Coefficients:
    Estimate Std. Error t value Pr(>|t|)
x1n   1.1018     0.2266   4.863 4.03e-05 ***
x2n   1.2426     0.2398   5.181 1.69e-05 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 3.647 on 28 degrees of freedom
Multiple R-squared:  0.6383,	Adjusted R-squared:  0.6124
F-statistic:  24.7 on 2 and 28 DF,  p-value: 6.572e-07

We can't tell this

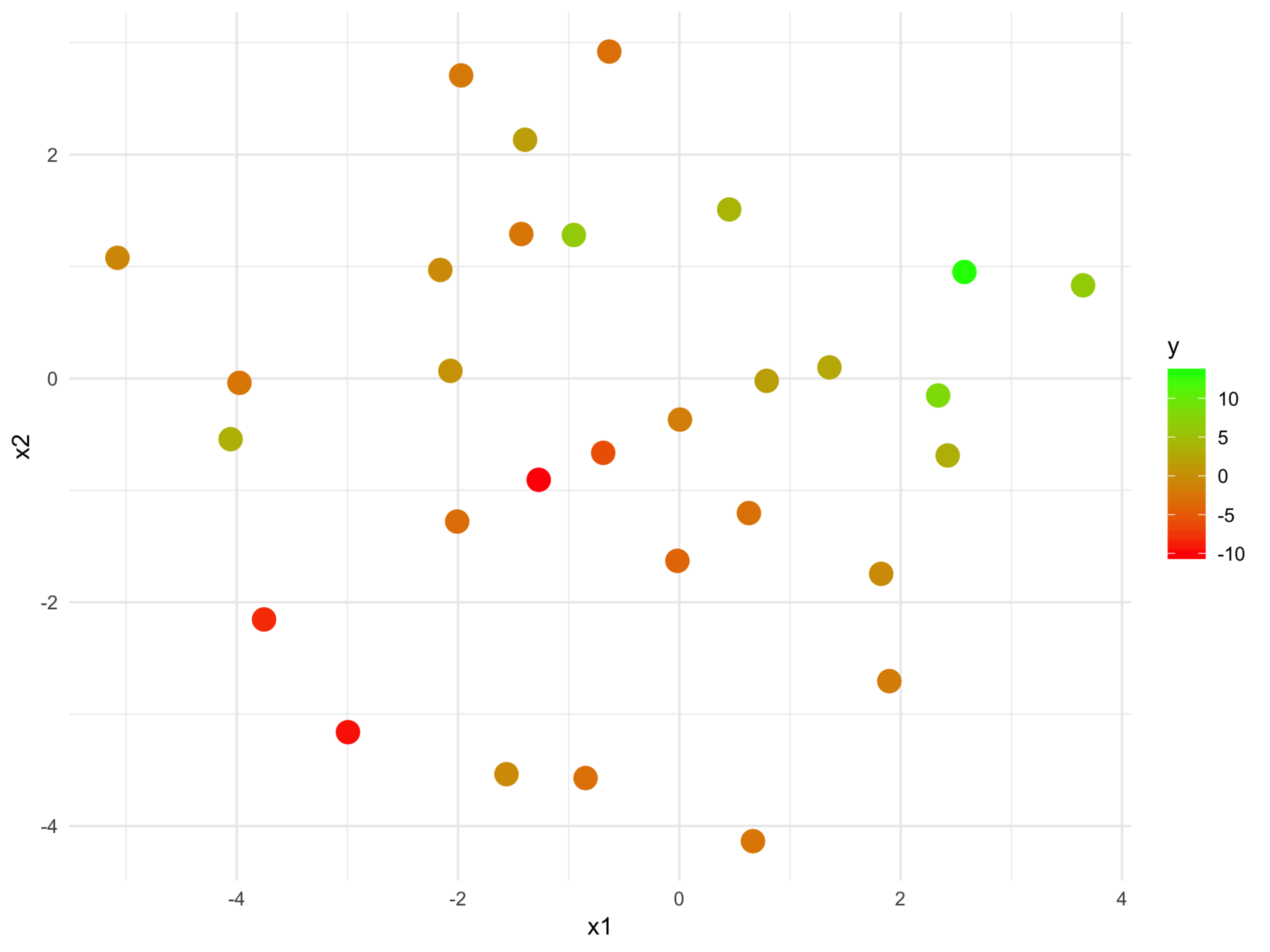
from this

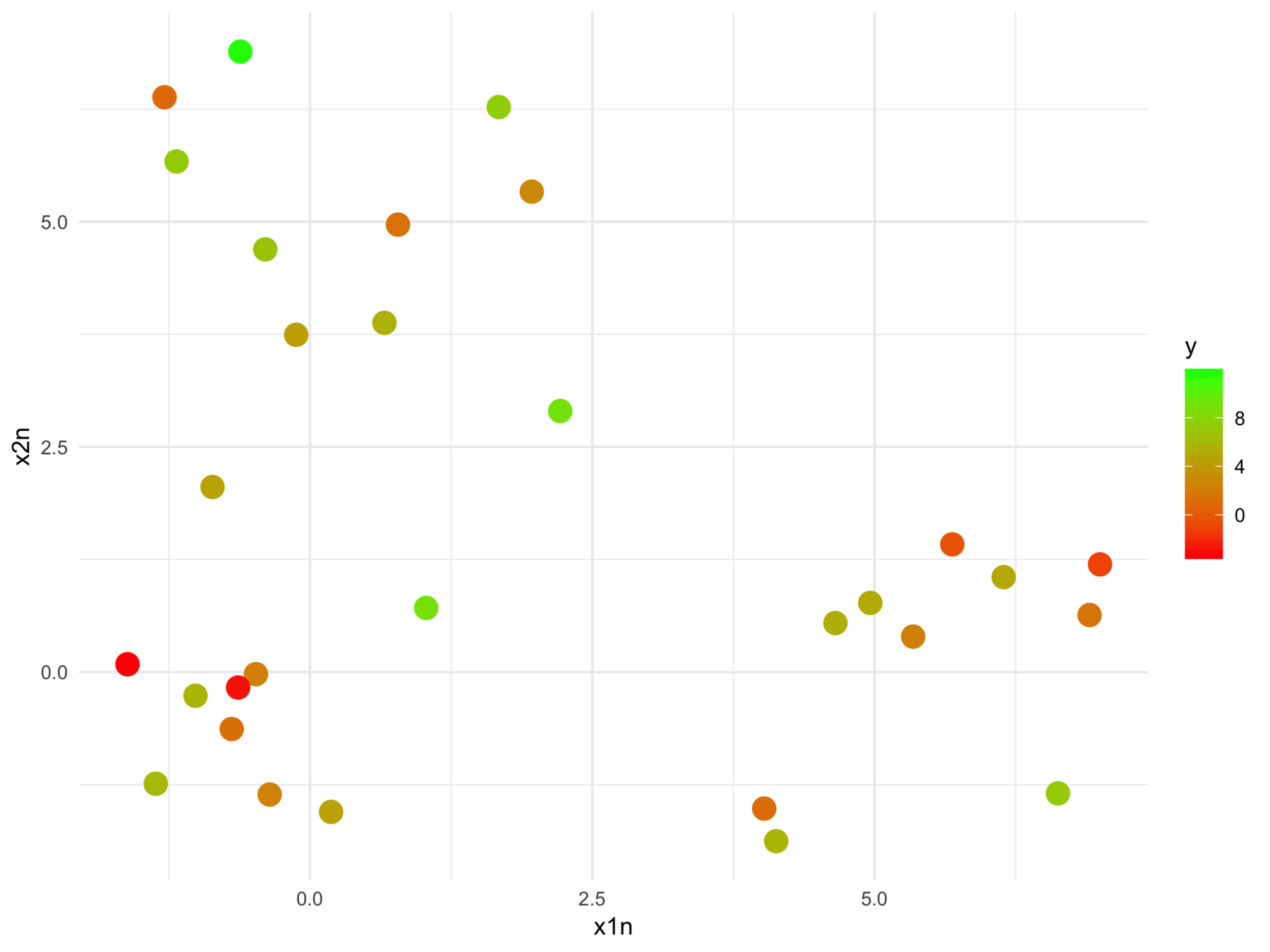
The model fits relationships between the regressors and the outcome

 

But we may want the relationships between the regressors with respect to the outcome

More formally start with supervised learning:

Consider \( n \) training samples \( \{x_1, x_2, .., x_n\} \), each with \(p\) features.

 

Given a response vector \(\{y_1, y_2, ..., y_n\}\), find a function \(h : \mathcal{X} \rightarrow \mathcal{Y}\) minimizing the \(\sum_{i=1}^{n} L( h(x_i), y)\) with respect to a loss function \(L\).

Construct \(h = f \circ g_y \) such that \(g_y  : \mathcal{X} \rightarrow \mathcal{X'} \)  is a latent space projection of the original data, whose geometry is dictated by the response.


Note that \(f\) is not parameterized by the response.

...and construct a (supervised) latent space 

Let \(X \in \mathcal{R}^{n \times p}\) be a full-rank design matrix with \(n > p\), \(X = U \Sigma V\) is the singular value decomposition of \(X\). 

 

 

where \(\Gamma\) is a diagonal matrix in \(\mathcal{R}^{p \times p}\), \(\mathbf{1}\) is a column of ones in \(\mathcal{R}^n\), and \(\varepsilon\) is composed of (sufficiently) i.i.d. samples from a random variable with mean zero and standard deviation \(\sigma\).

 

A simple example with OLS

Y = X V \Gamma \mathbf{1} + \varepsilon
Y=XVΓ1+εY = X V \Gamma \mathbf{1} + \varepsilon

Under the \(\ell^2\) loss function we can find the optimal value of \(\widehat \Gamma\) among the set of all weight matrices \(\tilde \Gamma\) with

 

 

 

 

The matrix \(\widehat \Gamma\) is \(\text{diag}(\widehat \beta)\) where \(\widehat \beta = \Sigma^{-1} U^T Y\) is the slope coefficient estimates of the corresponding linear model.

A simple example with OLS

\widehat \Gamma = \underset{\tilde \Gamma}{\operatorname{argmin}} \ ||Y - X V \tilde \Gamma \mathbf{1} ||
Γ^=argmin⁡Γ~ ∣∣Y−XVΓ~1∣∣\widehat \Gamma = \underset{\tilde \Gamma}{\operatorname{argmin}} \ ||Y - X V \tilde \Gamma \mathbf{1} ||

\(X_Y = XV \tilde \Gamma\) represent the data in the latent space

 

Each column whose corresponding slope coefficient is not zero, contributes equally to the estimate of \(Y\) in expectation

A simple example with OLS

If the distance metric denoted by matrix \(A \in \mathcal{R}^{p \times p}\) and the distance between any two \(1 \times p\) matrices \(x\) and \(y\) expressed by

 

 

The square euclidean distance between two samples, \(i\) and \(j\) in \(X_Y\), denoted as \(X_Y(i)\) and \(X_Y(j)\) respectively is
 

A metric learning connection

d_A^2(x, y) = ||x - y||_A = (x - y) A (x - y)^T
dA2(x,y)=∣∣x−y∣∣A=(x−y)A(x−y)Td_A^2(x, y) = ||x - y||_A = (x - y) A (x - y)^T
|| X_Y(i) - X_Y(j) ||^2 = || X(i)V - X(j)V ||_{\Gamma}^2
∣∣XY(i)−XY(j)∣∣2=∣∣X(i)V−X(j)V∣∣Γ2|| X_Y(i) - X_Y(j) ||^2 = || X(i)V - X(j)V ||_{\Gamma}^2

A bias-corrected Gramian matrix estimate

\mathbb{P} X_Y X_Y^T - \sigma^2 \text{I} = U (\Sigma \Gamma)^2 U^T
PXYXYT−σ2I=U(ΣΓ)2UT\mathbb{P} X_Y X_Y^T - \sigma^2 \text{I} = U (\Sigma \Gamma)^2 U^T
\begin{aligned} \mathbb{P} \, X_Y X_Y^T & = \mathbb{P} \, U \, \Sigma \, \widehat \Gamma^2 \, \Sigma \, U^T \\ &= \mathbb{P} \, U \Sigma (\Gamma + \sigma \Sigma^{-1} \mathbf{Z})^2 \Sigma U^T \\ & = \mathbb{P} \, U (\Sigma^2 \Gamma^2 + 2 \sigma \Gamma \Sigma \mathbf{Z} + \sigma^2 \mathbf{Z}^2) U^T \\ \end{aligned}
P XYXYT=P U Σ Γ^2 Σ UT=P UΣ(Γ+σΣ−1Z)2ΣUT=P U(Σ2Γ2+2σΓΣZ+σ2Z2)UT\begin{aligned} \mathbb{P} \, X_Y X_Y^T & = \mathbb{P} \, U \, \Sigma \, \widehat \Gamma^2 \, \Sigma \, U^T \\ &= \mathbb{P} \, U \Sigma (\Gamma + \sigma \Sigma^{-1} \mathbf{Z})^2 \Sigma U^T \\ & = \mathbb{P} \, U (\Sigma^2 \Gamma^2 + 2 \sigma \Gamma \Sigma \mathbf{Z} + \sigma^2 \mathbf{Z}^2) U^T \\ \end{aligned}

Proof:

Let \(\mathbf{Z}\) be a diagonal matrix of standard normals​

A toy example with iris

> head(iris)
  Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1          5.1         3.5          1.4         0.2  setosa
2          4.9         3.0          1.4         0.2  setosa
3          4.7         3.2          1.3         0.2  setosa
4          4.6         3.1          1.5         0.2  setosa
5          5.0         3.6          1.4         0.2  setosa
6          5.4         3.9          1.7         0.4  setosa
> 
> fit <- lm(Sepal.Length ~, iris[,-5])

A toy example with iris

> mm <- model.matrix(Sepal.Length ~ ., iris[,-5])
> 
> km <- kmeans(mm, centers = 3)
> table(km$cluster, iris$Species)
   
    setosa versicolor virginica
  1     21          1         0
  2     29          2         0
  3      0         47        50
>
> # ...
> table(subgroups$membership, iris$Species)
   
    setosa versicolor virginica
  1     50          0         0
  2      0         23         0
  3      0         27        20
  4      0          0        30

Comparison with K-means

> mm <- model.matrix(Sepal.Length ~ ., iris[,-5])
> 
> km <- kmeans(mm, centers = 4)
> table(km$cluster, iris$Species)

    setosa versicolor virginica
  1      0         24         0
  2     50          0         0
  3      0          0        36
  4      0         26        14
>
> # ...
> table(subgroups$membership, iris$Species)
   
    setosa versicolor virginica
  1     50          0         0
  2      0         23         0
  3      0         27        20
  4      0          0        30

Comparison with K-means

Back to cancer

Clinical trial data is not low-dimensional

 

Sometimes the predictive information isn't in a linear subspace of the data

Anonymous drug 1

Received "accelerated approval"

 

Response rate was high, but not quite as high as expected

 

Subtype response based on baseline characteristics

All Trajectories

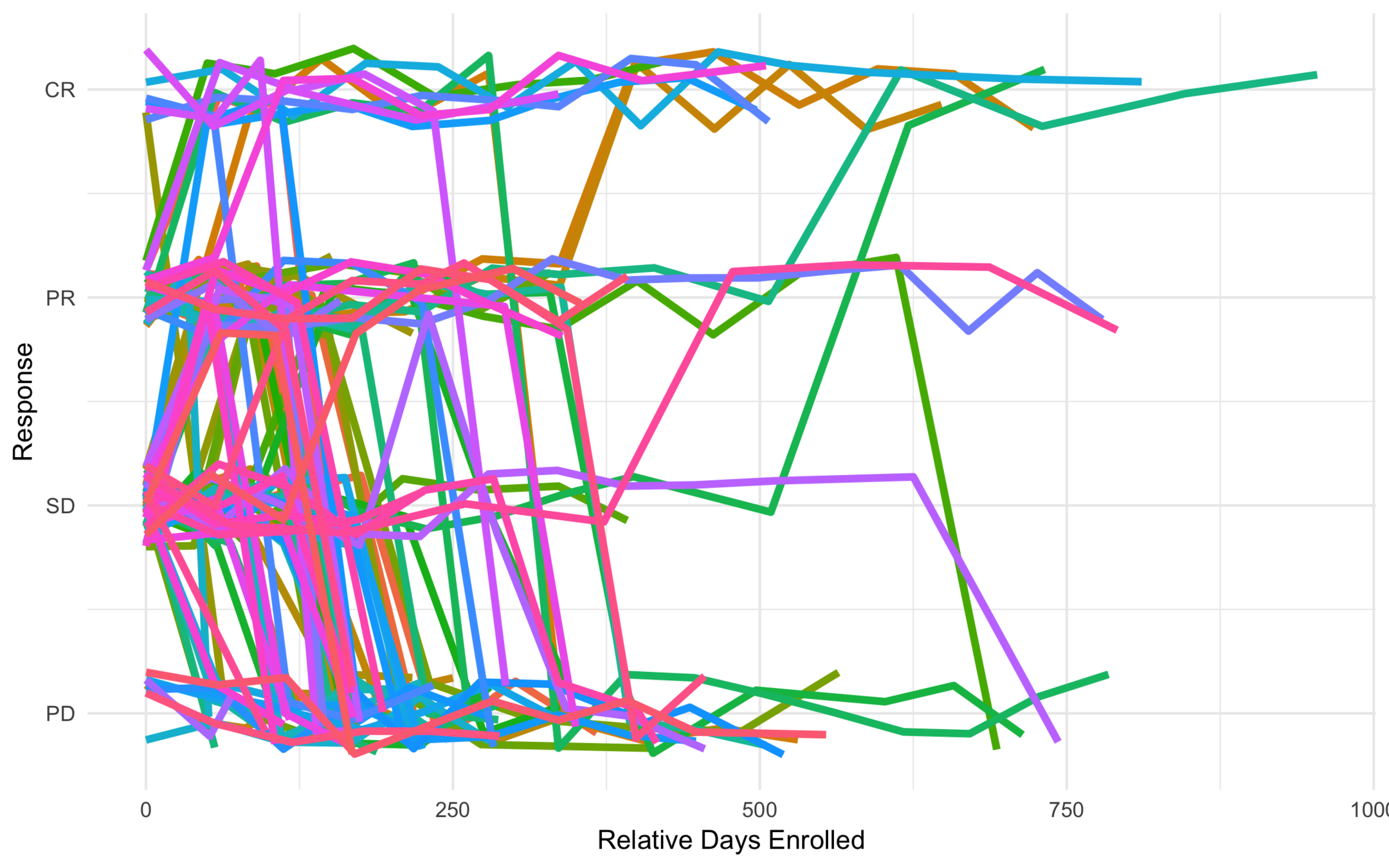
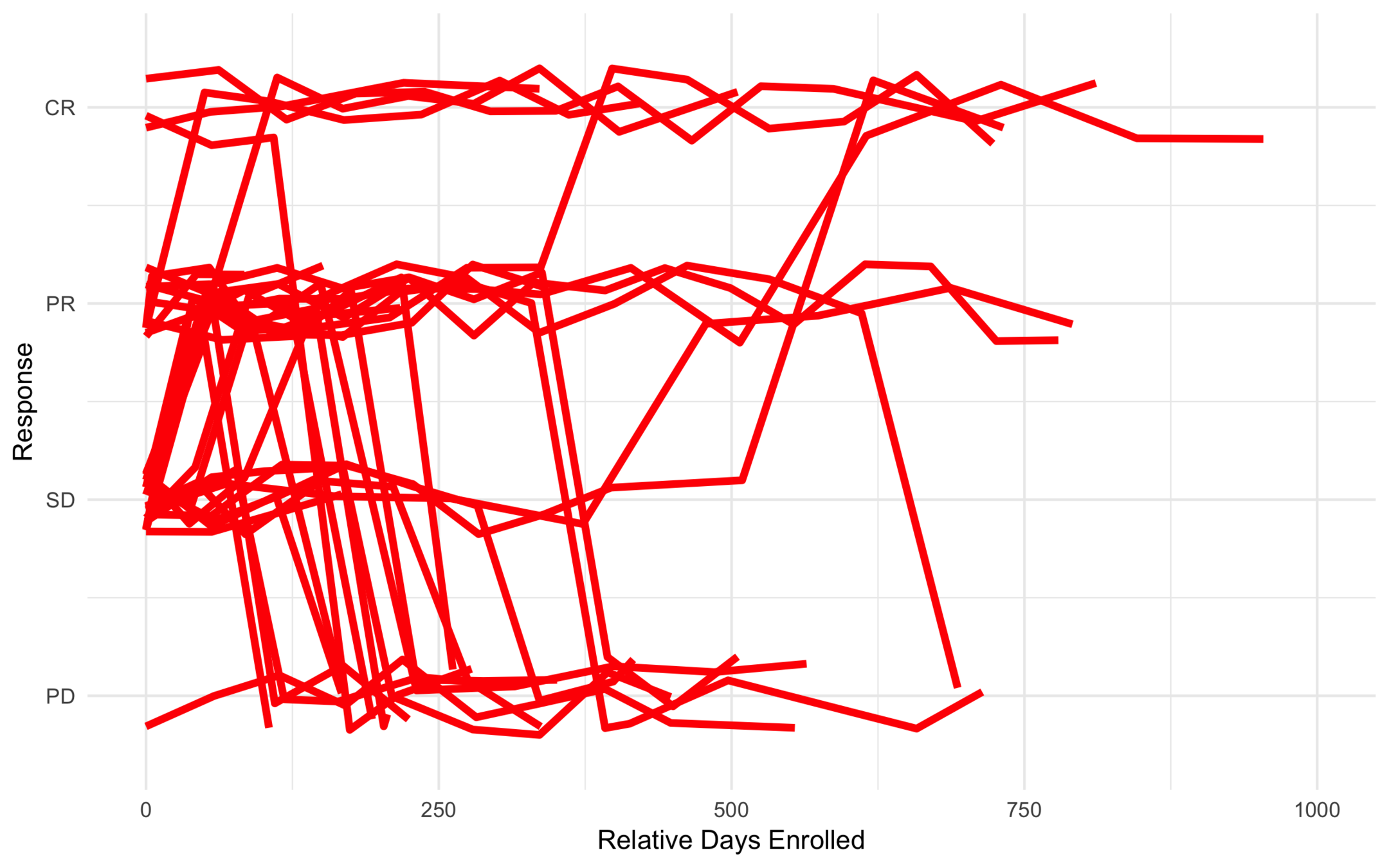
Low Risk

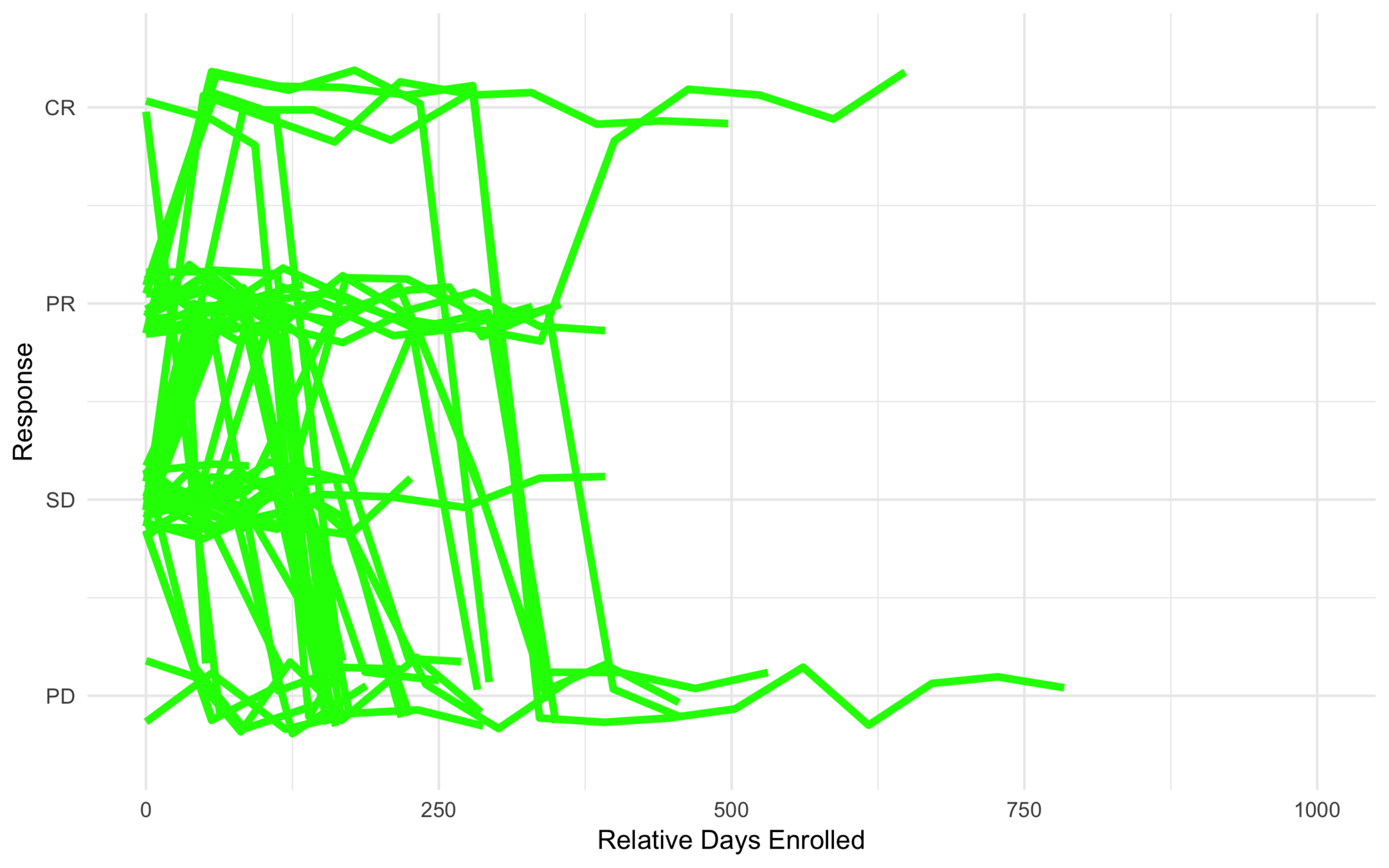
Intermediate Risk

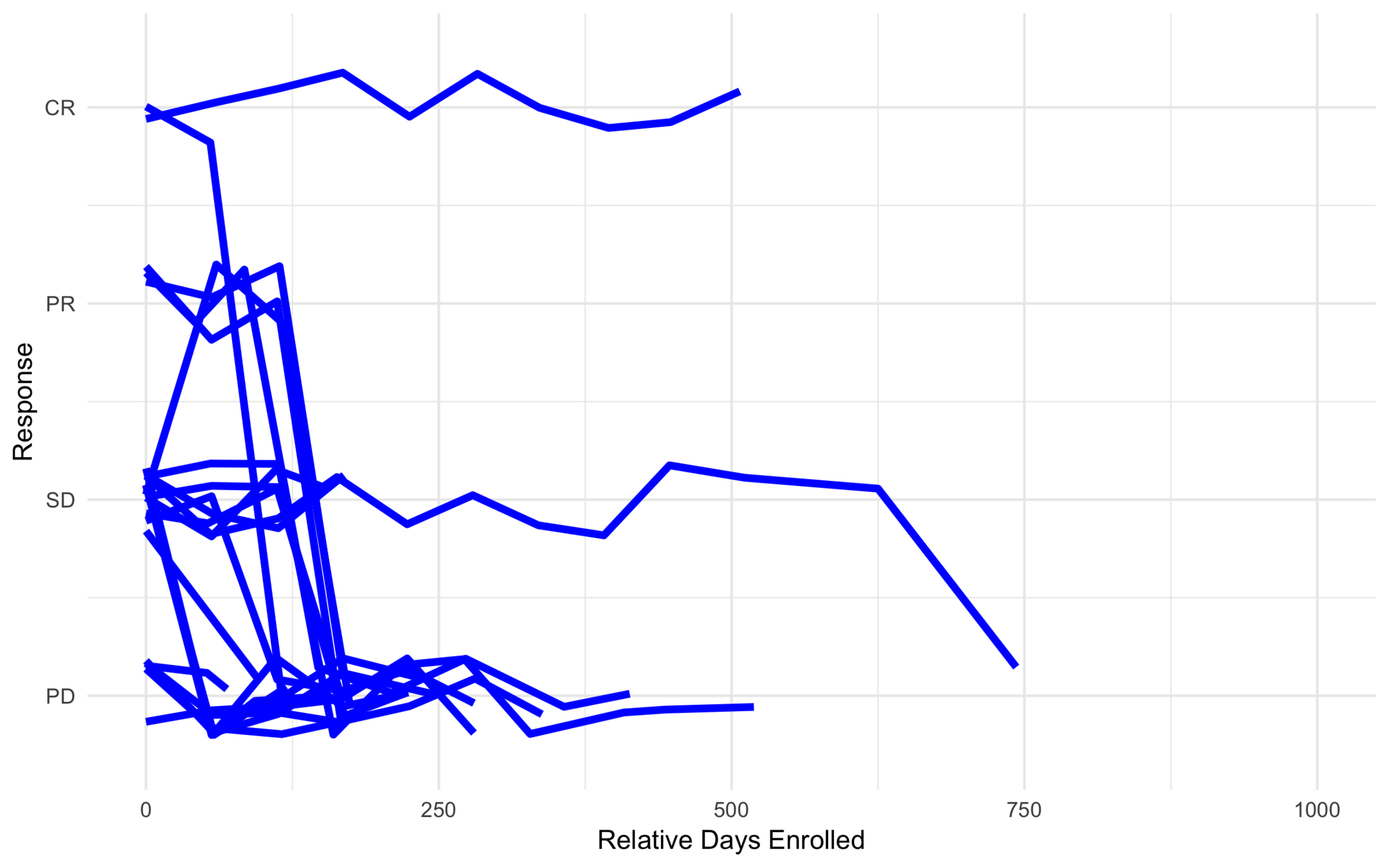
High Risk

Anonymous Drug 1

Was found to be effective for a certain type of cancer.

 

Ran into problems with severe toxicity events (449 toxicities out of 607).

 

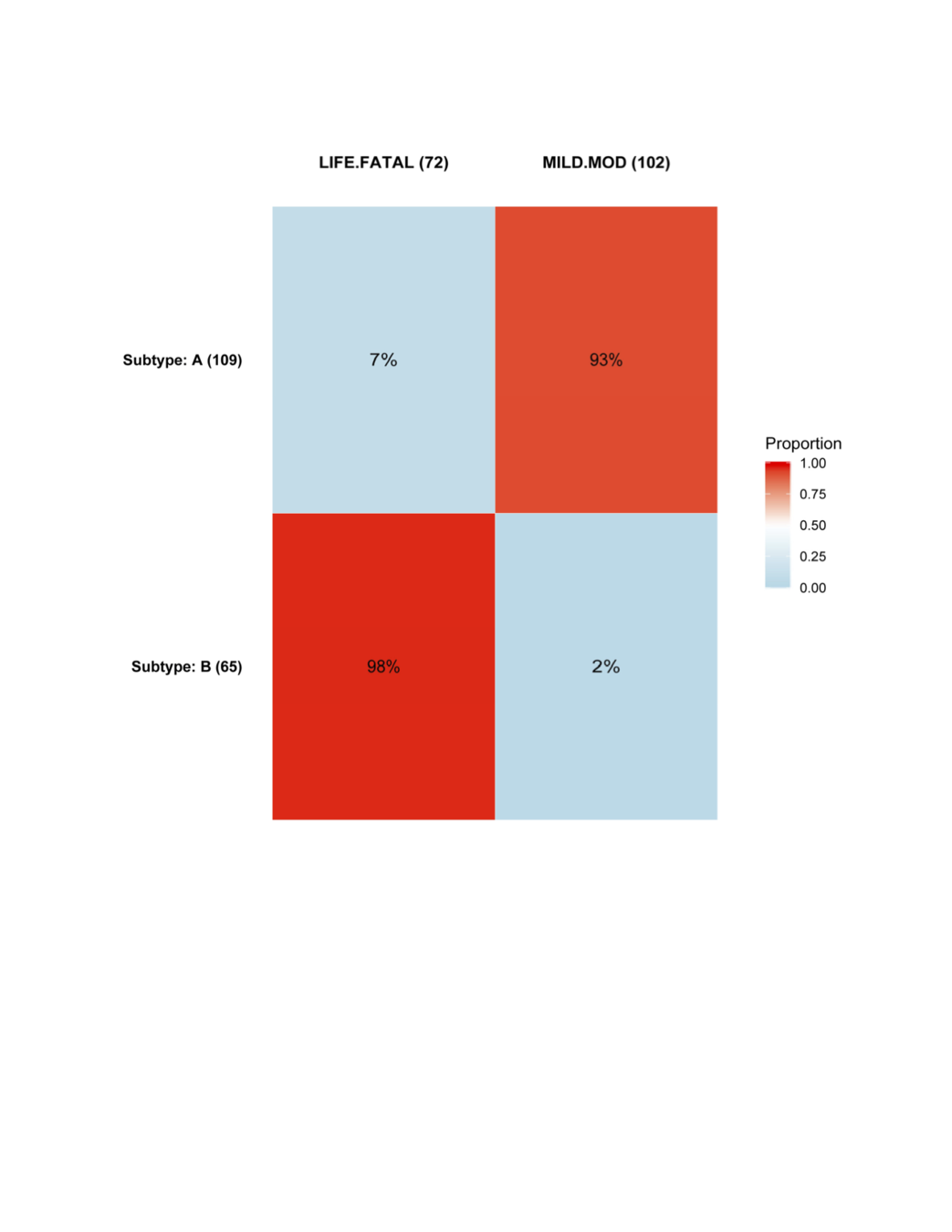
Goal was to find subtypes least (or most) likely to have toxicity events.

Variable Description
AMD19FL ​Exon 19 Del. Act. Mut. Flag
AM858FL L858R Activating Mut. Flag
LIVERFL Mets Disease Site Liver Flag
DISSTAG Disease Stage at entry 
NUMSITES Num. of Mets Disease Sites 
PRTK ​Number of Prior TKI
PRTX ​Number of Prior Therapies
​WTBL Baseline Weight
SEX

AE Heatmap

AE Similarity Network

What else can you do with subtyping?

1. Improve prediction accuracy:

  • Recall \(g_y  : \mathcal{X} \rightarrow \mathcal{X'} \)
  • Combine new samples with an \(f\) parameterized by \(Y\), \(h' = f_y \circ g_y \)
  • E.g. Bayesian power prior​

​ 

2. Construct counterfactuals and create synthetically controlled trials.

  • Obtain data from other trials (standard of care)
  • Project data into the latent space
  • Match
  • Compare results

Thanks