glmnetlib: A Low-level Library for Regularized Regression

pirls: An R/C++ Package for Penalized, Iteratively Reweighted Least Squares Regression

Goals

Talk: show how many different regression routines (especially glmnet) fit together

 

Package: write a package that is:

  - fast enough to be used

  - simple enough to use and understand

  - extensible enough to create new routines

 

Why should we still care about linear models?

Fitting has relatively low complexity

 

We can figure out how and when they don't work

 

They are compatible with other learners

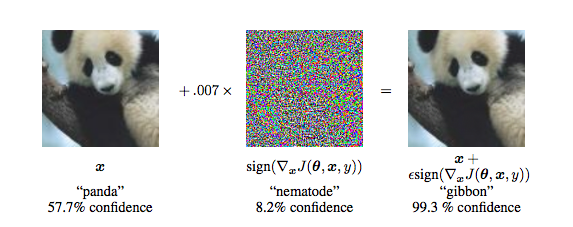
Breaking DL with Adversarial Noise

Figure from Explaining and Harnessing Adversarial Examples by Goodfellow et al.

> train_inds = sample(1:150, 130)
> iris_train = iris[train_inds,]
> iris_test = iris[setdiff(1:150, train_inds),]
> lm_fit = lm(Sepal.Length ~ Sepal.Width+Petal.Length,  
+             data=iris_train)
> sd(predict(lm_fit, iris_test) - iris_test$Sepal.Length)
[1] 0.3879703
> library(randomForest)
> iris_train$residual = lm_fit$residuals
> iris_train$fitted_values = lm_fit$fitted.values
> rf_fit = randomForest(
+   residual ~ Sepal.Width+Petal.Length+fitted_values,  
+   data=iris_train)
> 
> lm_pred = predict(lm_fit, iris_test)
> iris_test$fitted_values = lm_pred
> sd(predict(rf_fit, iris_test)+lm_pred - 
+   iris_test$Sepal.Length)
[1] 0.3458326
> rf_fit2 = randomForest(
+   Sepal.Length ~ Sepal.Width+Petal.Length,
+   data=iris_train)
> sd(predict(rf_fit2, iris_test) - iris_test$Sepal.Length)
[1] 0.40927

What is glmnet?

\text{regressor matrix:\ \ } X \in \mathcal{R}^{n \times p}
\text{dependent data:\ \ } y \in \mathcal{R}^n
\text{slope coefficient estimates:\ \ } \hat \beta \in \mathcal{R}^p
\text{penalty parameter:} \lambda \in [0, \infty)
\text{elastic net parameter:} \alpha \in [0, 1]

Notation:

\text{a weight matrix:} W \in R^{n \times n}
\text{a link function:} g
\min_{\hat{\beta}} ||W^{1/2} (y - g(X \hat \beta))||^2 + (1-\alpha) \frac{\lambda}{2} ||\hat \beta||^2 + \alpha \lambda ||\hat \beta||_1

Find:

The Ridge Part

The Least Absolute Shrinkage and Selection Operator (LASSO) Part

Why (re)implement glmnet?

Afterall....

  - it is standard

  - it is fast

However....

  - it does not support arbitrary family-link combinations

  - it's not designed for out-of-core

  - it is written mostly in mortran

mike@Michaels-MacBook-Pro-2:~/projects/glmnet/inst/mortran
> wc -l glmnet5.m 
    3998 glmnet5.m
mike@Michaels-MacBook-Pro-2:~/projects/glmnet/inst/mortran
> head -n 1000 glmnet5.m | tail -n 20
            if g(k).gt.ab*vp(k) < ix(k)=1; ixx=1;>
         >
         if(ixx.eq.1) go to :again:;
         exit;
      >
      if nlp.gt.maxit < jerr=-m; return;> 
      :b: iz=1;
      loop < nlp=nlp+1; dlx=0.0;
         <l=1,nin; k=ia(l); gk=dot_product(y,x(:,k));
            ak=a(k); u=gk+ak*xv(k); v=abs(u)-vp(k)*ab; a(k)=0.0;
            if(v.gt.0.0)
               a(k)=max(cl(1,k),min(cl(2,k),sign(v,u)/(xv(k)+vp(k)*dem)));
            if(a(k).eq.ak) next;
            del=a(k)-ak; rsq=rsq+del*(2.0*gk-del*xv(k));
            y=y-del*x(:,k); dlx=max(xv(k)*del**2,dlx);
         >
         if(dlx.lt.thr) exit; if nlp.gt.maxit < jerr=-m; return;>
      >
      jz=0;
   >

lewis_glm = function(X, y, lambda, alpha=1, family=binomial, maxit=500, 
                     tol=1e-8, beta=spMatrix(nrow=ncol(X), ncol=1)) {
  converged = FALSE
  for(i in 1:maxit) {
    eta      = as.vector(X %*% beta)
    g        = family()$linkinv(eta)
    gprime   = family()$mu.eta(eta)
    z        = eta + (y - g) / gprime
    W        = as.vector(gprime^2 / family()$variance(g))
    beta_old = beta
    beta = solve(crossprod(X, W*X), crossprod(X, W*z))
    if(sqrt(as.vector(Matrix::crossprod(beta-beta_old))) < tol) {
      converged = TRUE
      break
    }
  }
  list(beta=beta, iterations=i, converged=converged)
}

Start with Bryan Lewis' GLM implementation

pirls = function(X, y, lambda, alpha=1, family=binomial, maxit=500, 
                 tol=1e-8, beta=spMatrix(nrow=ncol(X), ncol=1), 
                 beta_update=coordinate_descent) {
  converged = FALSE
  for(i in 1:maxit) {
    eta      = as.vector(X %*% beta)
    g        = family()$linkinv(eta)
    gprime   = family()$mu.eta(eta)
    z        = eta + (y - g) / gprime
    W        = as.vector(gprime^2 / family()$variance(g))
    beta_old = beta
    beta = beta_update(X, W, z, lambda, alpha, beta, maxit)
    if(sqrt(as.vector(Matrix::crossprod(beta-beta_old))) < tol) {
      converged = TRUE
      break
    }
  }
  list(beta=beta, iterations=i, converged=converged)
}

 Make the slope update a function

coordinate_descent = function(X, W, z, lambda, alpha, beta, maxit) {
  quad_loss = quadratic_loss(X, W, z, lambda, alpha, beta)
  for(i in 1:maxit) {
    beta_old = beta
    quad_loss_old = quad_loss
    beta = update_coordinates(X, W, z, lambda, alpha, beta)
    quad_loss = quadratic_loss(X, W, z, lambda, alpha, beta)
    if(quad_loss >= quad_loss_old) {
      beta = beta_old
      break
    }
  }
  if (i == maxit && quad_loss <= quad_loss_old) {
    warning("Coordinate descent did not converge.")
  }
  beta
}

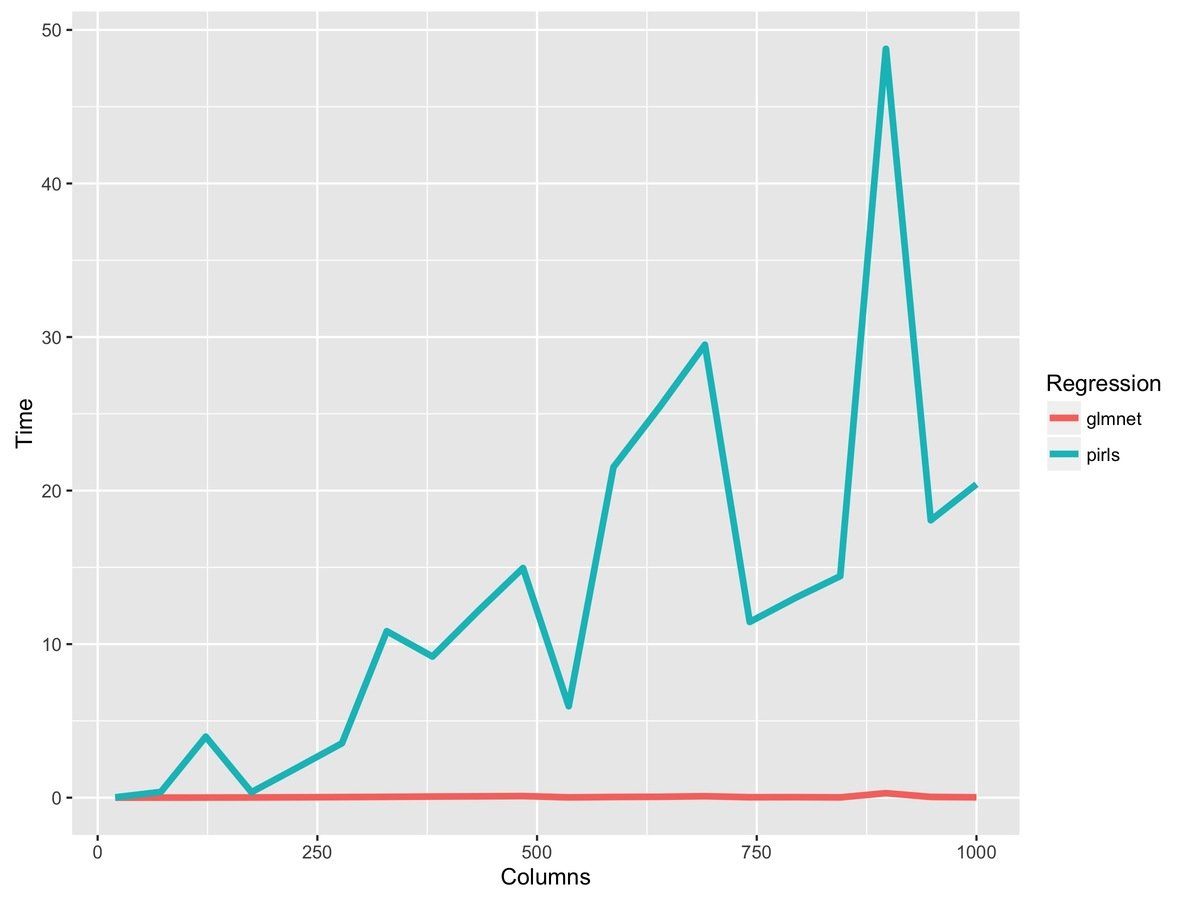
> summaryRprof("pirls_profile.out")
...
$by.total
                     total.time total.pct self.time self.pct
"beta_update"              1.06    100.00      0.00     0.00
"pirls"                    1.06    100.00      0.00     0.00
"update_coordinates"       1.06    100.00      0.00     0.00

Where are spending all of our time?

"Because you're a C++ programmer, there's an above-average chance you're a performance freak. If you're not you're still probably sympathetic to their point of view. (If you're not at all interested in performance, shouldn't you be in the Python room down the hall?)"

-- Scott Meyers, Effective Modern C++

update_coordinates = function(X, W, z, lambda, alpha, beta) {
  beta_old = beta
  for (i in 1:length(beta)) {
    beta[i] = soft_thresh_r(sum(W*X[,i]*(z - X[,-i] %*% beta_old[-i])),
                               sum(W)*lambda*alpha)
  }
  beta / (colSums(W*X^2) + lambda*(1-alpha))
}

template<typename ModelMatrixType, typename WeightMatrixType,
         typename ResponseType, typename BetaMatrixType>
double update_coordinate(const unsigned int i,
  const ModelMatrixType &X, const WeightMatrixType &W, const ResponseType &z,
  const double &lambda, const double &alpha, const BetaMatrixType &beta,
  const double thresh) {
  ModelMatrixType X_shed(X), X_col(X.col(i));
  BetaMatrixType beta_shed(beta);
  X_shed.shed_col(i);
  beta_shed.shed_row(i);
  double val = arma::mat((W*X_col).t() * (z - X_shed * beta_shed))[0];
  double ret = soft_thresh(val, thresh);
  if (ret != 0)
    ret /= accu(W * square(X_col)) + lambda*(1-alpha);
  return ret;
}

Substitute this...

for this...

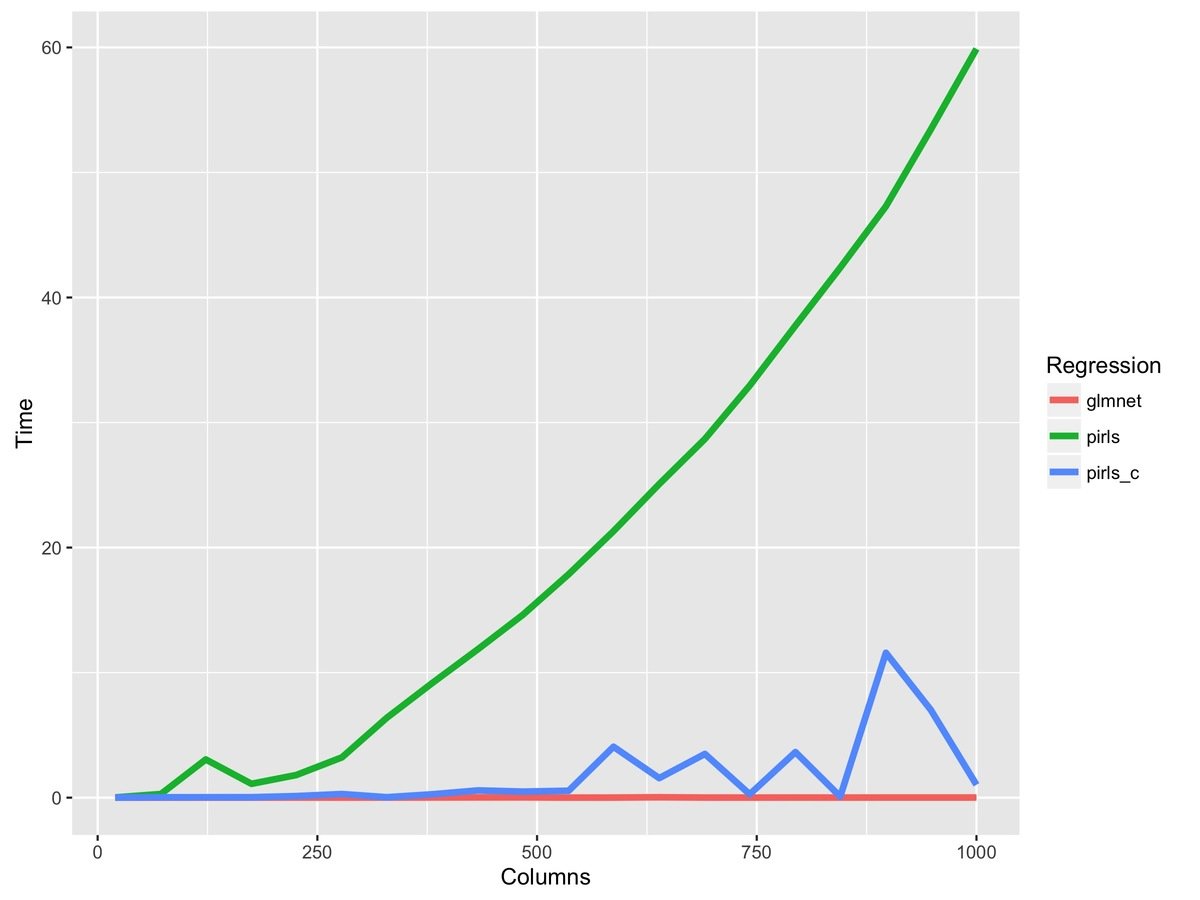
fit_r = pirls(x, y, lambda=lambda, family=gaussian)

R code changes from this...

to this...

fit_rc = pirls(x, y, lambda=lambda, family=gaussian, 
               beta_update=c_coordinate_descent)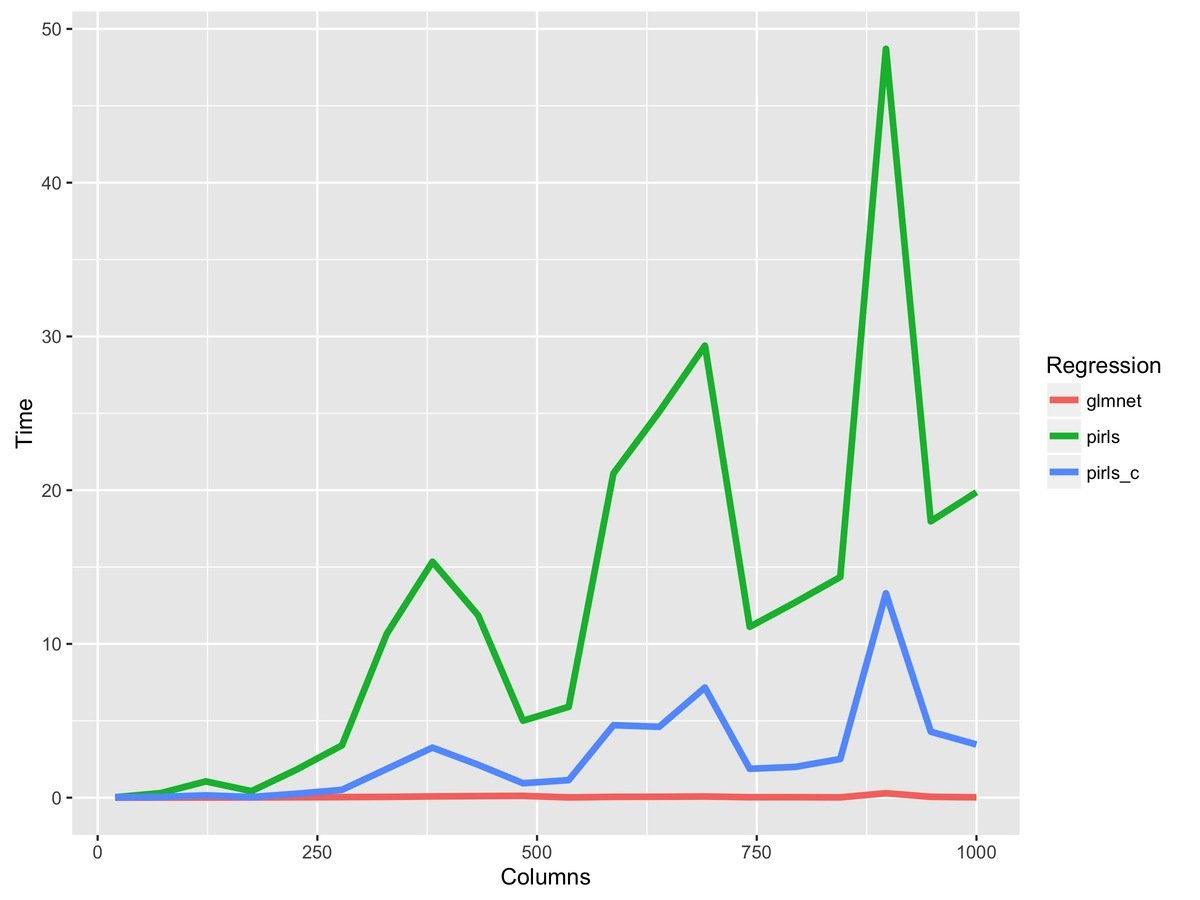

The first rule of fitting high-dimensional models is you don't fit high-dimensional models

Prefilter Regressors

SAFE - discard the jth variable if 

|x_j^T y|/n > \lambda - \frac{||x_2|| ||y_2||}{n} \frac{\lambda_{\text{max}} - \lambda}{\lambda_{\text{max}}}

STRONG - discard if KKT conditions are met and

|x_j^T y|/n > 2 \lambda - \lambda_{\text{max}}

pirls

Models supported:

  - OLS, GLM, Ridge, LASSO, Elastic net

  - need a little more infrastructure for "m" regressions


Still in development but available on Github at https://github.com/kaneplusplus/pirls


Some experimental multi-threaded functionality


Plan for out-of-core